Assignment 8: LightEmAll🔗

Goals: Design a game with mutable world state, ArrayLists, and loops. Learn a new kind of data structure and experiment with algorithms on that structure.

You will be using the Impworld library, as in Recitation 10 — make sure that at the top of your file, you include

Make sure you do not name any of your files World.java, or else the autograder will not be able to compile your code.

Instructions🔗

This assignment is long. Start early.

You will complete two parts of this assignment. You will submit only the final version. Submit all the files needed for your game, in one .zip file.

The two portions are as follows:

Part 1 You must complete the task of designing and implementing the GamePiece class — this includes connecting GamePieces to neighboring GamePieces, drawing GamePieces, and the click-to-rotate behavior. Your board will be manually generated.

Part 2 You must complete the power-up behavior (where the power station has some finite radius of effectiveness), drawing the powered lines, and moving the power station when the arrow keys are pressed. You will generate a fractal-like board using a subdivision algorithm.

Due: Tuesday December 16 at 10:00pm.

Gameplay🔗

This assignment is based on a game called Power Line. The main difference is that our power station has some finite radius of effectiveness, and must be moved to ensure power reaches every tile.

You goal is to light up every tile of the board, by ensuring that all the wires are connected to the power station. Initially, the board has been scrambled by randomly rotating each tile:

You can click to rotate tiles to join the wires together, but you cannot move tiles:

However, there is more to the puzzle — the station is only effective up to a finite radius, and tiles beyond that radius will be unpowered:

Therefore, you will have to use the arrow keys to move the power station. Furthermore, the power station must follow the path created by the wiring. The player wins when all the tiles are lit up:

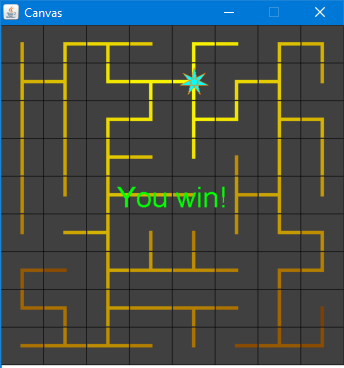
1 Tasks🔗

Here is the list of tasks you will need to complete to implement the game.

1.1 Setting up the game🔗

You will need to create a two-dimensional grid of GamePieces to represent the board. The width and height of the board should be specified as arguments to your LightEmAll constructor. You must include at least one constructor, LightEmAll(int width, int height), which interprets width and height as tile counts, and constructs a valid board with all fields initialized and scrambled, so the initial game is not already solved.

Because the size of the board is configurable, you cannot simply hard-code lists of data, because they may be of the wrong size. Instead, you’ll need to use loops and ArrayLists.

In addition, your board field must satisfy these invariants:

• There must be exactly one tile with powerStation == true, and that tile is precisely board.get(powerCol).get(powerRow).

• width and height are the number of tiles in each direction, not pixels.

• board is column-major: board.get(c).get(r) is the tile at column c, row r.

• board.size() == width, and for every column c, board.get(c).size() == height.

• For every tile gp = board.get(c).get(r), we must have gp.col == c and gp.row == r.

Effectively, we have created a graph, where each GamePiece is a node and the wires are edges.

Each GamePiece represents a tile on the board, and has wires extending to adjacent GamePieces. The boolean fields left, right, top, and bottom indicate which neighboring GamePieces can be connected. Your GamePiece must have at least these fields:

For example, the following GamePiece has left, right, and bottom set to true:

A GamePiece may also have a power station, which supplies power to all reachable GamePieces, up to an effective radius, where the radius is defined as \((diameter / 2) + 1\). To compute the diameter of your graph, first run breadth-first search (see below) to determine the last-found GamePiece. Next, run breadth-first search starting from that last-found piece and count the depth to the new last-found piece again. That depth is the diameter of the graph.

The initial position of the power station will depend on which board generation strategy you are using.

Your GamePiece class must provide at least the constructor

which sets those fields and initializes powerStation to false.

The specific wiring of the board can be thought of as a “maze”, which is generated by one of two strategies, discussed below. After this step is complete, the game will shuffle the board, by applying a random number of rotations to each GamePiece.

For autograding, your classes must provide the following methods with exactly these signatures. You may represent which tiles are powered however you like (e.g. as a field in each GamePiece, a separate data structure, or computed on demand). However, for testing you must implement:

• GamePiece.rotate(), which rotates the tile 90 degrees clockwise, i.e., updates left, right, top, and bottom in place.

• WorldImage GamePiece.tileImage(int size, int wireWidth, Color wireColor, boolean hasPowerStation), which produces an image of this tile, drawing wires according to the four boolean fields, and drawing a power-station marker when hasPowerStation is true.

• void LightEmAll.onMouseClicked(Posn pos), which treats the world as a grid of equal-sized tiles, and when the user clicks inside a tile, rotates that tile once clockwise.

• void LightEmAll.onKeyEvent(String key), which responds to "up", "down", "left", and "right" by attempting to move the power station one tile in that direction, but only if the move stays in bounds and the wires on the current and target tiles are connected in that direction. When a move succeeds, it must update powerRow, powerCol, and the two tiles’ powerStation flags.

• void LightEmAll.updatePower(), which recomputes which tiles are powered, given the current board wiring and power station location.

• boolean LightEmAll.isPoweredAt(int col, int row), which returns true exactly when the tile at column col, row row is currently receiving power.

• boolean LightEmAll.allPowered(), which returns true exactly when every tile in nodes is currently receiving power.

1.2 Board generation strategies🔗

There are two different board generation strategies to implement, one for each submission.

1.2.1 Manual generation🔗

For Part 1, the board will be manually generated, i.e., you will encode a specific board in the game logic, and every game will have the same solution. You should choose a simple pattern, such as all vertical lines with a single, horizontal bar through the center:

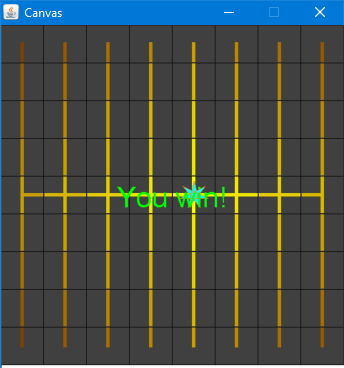
Or all horizontal lines with a single, vertical bar through the center:

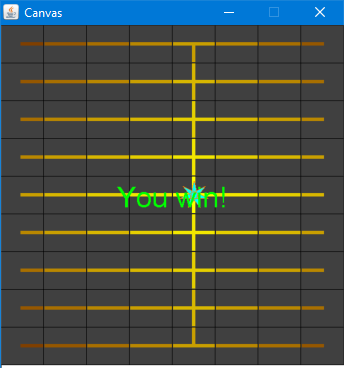
In both of these boards, the initial position of the power station should be at the center.

1.2.2 Fractal-like generation🔗

For Part 2, you will use a subdivision algorithm to generate fractal-like wiring.

The simplest board is a square whose sides are a power of two. The smallest such board is the base case: a 2×2 grid where the wires form a squared off U:

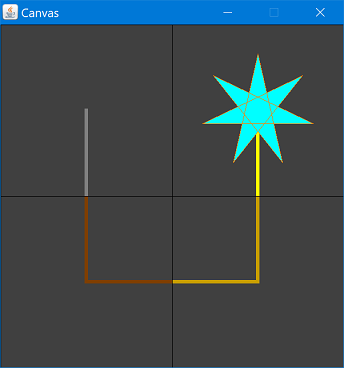
The next case is a 4×4 grid, where each quadrant is the 2×2 base case. Furthermore, the quadrants are connected in three locations: at the left, right, and bottom:

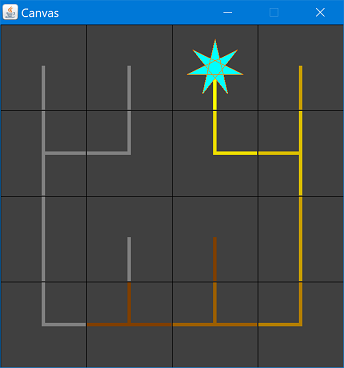
Of course, as the board size increases, the fractal becomes more and more complex:

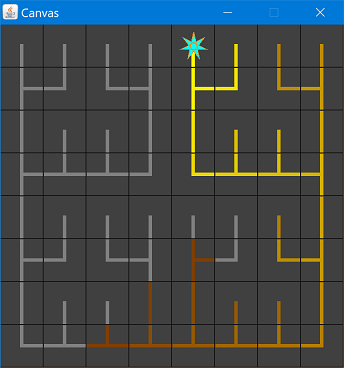
You’ll likely want to implement this algorithm in a “top-down” manner: start with a grid, subdivide it into four quadrants, recursively generate the wires in each quadrant, then connect the four quadrants.

The overall algorithm should be robust so that it can handle non-square grids and side lengths that are not powers of two.

Hint: Recall how binary search handles the base case. This will be very similar, but not exactly the same.

Initially, the power station should be located in the middle of the first row.